关系型数据库存储树形结构

2018-06-05

在日常开发中不免遇到需要在关系型数据库中存储树形结构数据的情况，这里介绍 3 种存储方法。

三种方法都以下面这个嵌套评论场景为背景。

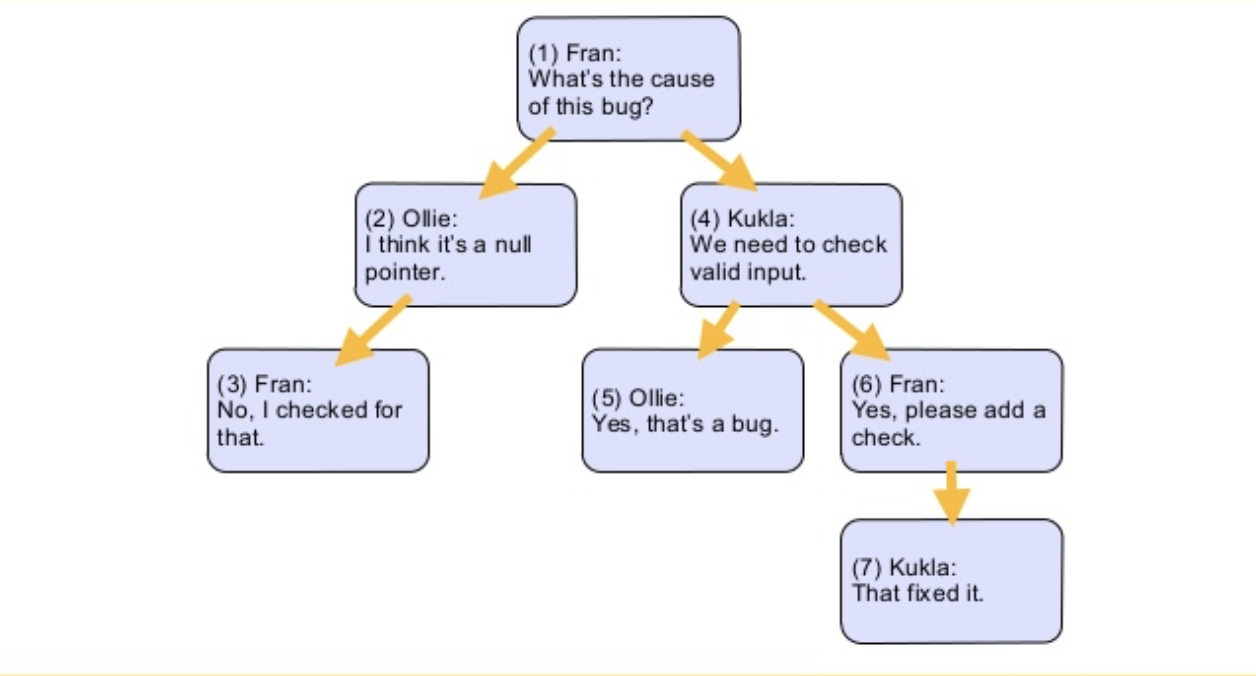
comment-hierarchy

Adjacency model(邻接模型)

这是最常见最简单的存储树形结构的方法了。每个元素都持有对父节点的引用作为外键(图中PK为主键，FK为外键)，是一个一对多的关系:

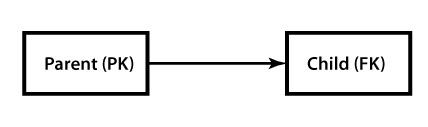
Adjacency model

添加/修改

添加和删除只要操作 parent_id 就可以了，添加到某节点就把 parent_id 设为该节点 id，从某节点下移动到另一个节点只要把 parent_id 更换为其他节点的 id 就可以了。

删除

使用 parent-child 方法需要删除节点就是比较复杂的了，因为不能简单地删除一个节点，这样属于该节点的子节点会找不到父节点，故而会出现一些问题，所以为了保持正确性得同时删除该节点的子节点。一种常见的做法是不直接删除该节点，而是标记该节点为删除状态，然后递归向下直到所有的后代都已经标记为删除了。

查询

查询直接的父节点或者子节点是非常容易的:

-- query a node's children
select *
from comments c1
  left join comments c2
    on (c2.parent_id = c1.id)

-- query a node's parent
select *
from comments c1
  join comments c2
    on (c1.parent_id = c2.id)

但是查询一颗子树的时候就比较麻烦了，这就需要递归查询，在性能上是很大的挑战。实现的方式有两种：

自顶向下查询，connect by 语法，这种方式较为简洁

-- query a node's subtree
select *
from comments
start with id=1
connect by parent_id = prior id
-- query a node's parent is the same

递归实现

1.第一步定义起始的点

select
  0 as depth,
  id,
  comment,
  parent_id
from comments
where id = 0

2.第二步定义每个子行与父节点之间关系

select
  parent.depth + 1,
  child.id,
  child.comment,
  child.parent_id
from recursive_query parent, comments child
where parent.id = child.parent_id

3.结合 1 2 步

with recursive_query(depth, id, comment, parent_id)
as (
select
  0 as depth,
  id,
  comment,
  parent_id
from comments
where id = 0
union all
select
  parent.depth + 1,
  child.id,
  child.comment,
  child.parent_id
from recursive_query parent, comments child
where parent.id = child.parent_id
)
select *
from recursive_query

元素数量和嵌套的层级

理论上元素数量和层级没有限制，可以有无数层。

Materialized Path(物化路径)

使用每个节点都存储祖先链的方式实现树的存储，这种方式很容易实现面包屑导航。

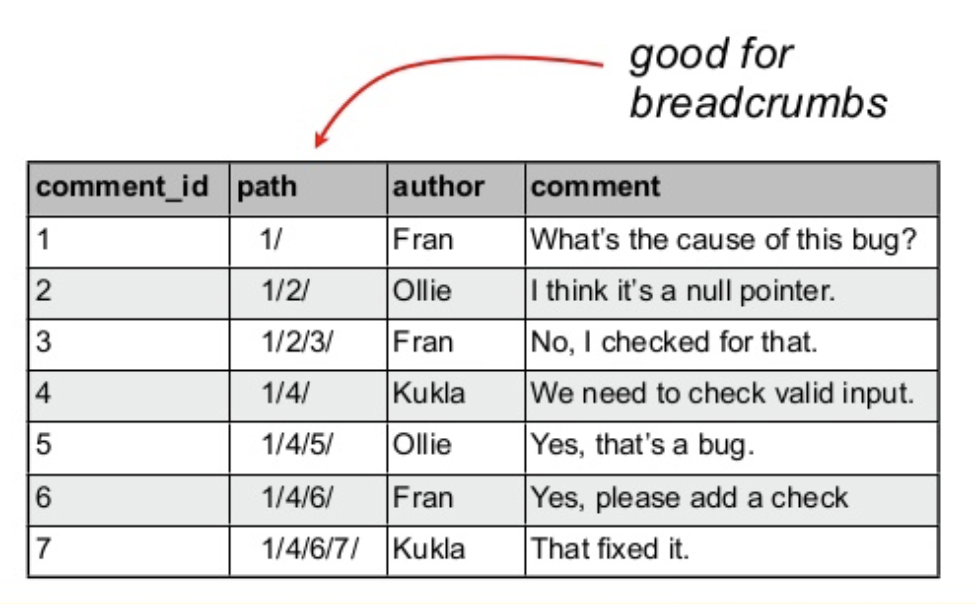
materialized path

添加/修改

添加一个节点，需要先获得父节点的 path，再在此基础上加上新节点的 id 组成新的 path来完成添加操作。

修改的话会更麻烦一点，需要更新该节点的 path 以及它的所有后代的 path。

删除

简单删除一个节点并不破坏整棵树的完整性，该节点的子节点虽然没有父级节点，但是有爷爷辈节点。

查询

查询一个节点下面的子树是非常容易的，直接 path like '{node's path}%' 就能选出来了，而不需要递归。

元素数量和嵌套的层级

元素的数量和嵌套的层级大小是取决于开发者的，事实上很少是需要无限的层级的：如果网站嵌套层级超过 20 层，那需要考虑重新设计了而不是盲目地增加层级了。

该模式的实现方式可以有很多种，比如点分割(1.1.2.5)或者斜杠分割(boss/chapter1/section2)，有时候规定一层的字符数量，空出来的空间用特殊字符填充(比如说0)，就像 000100020005 就表示 1/2/5 中间用 0 填充，这样每一层元素数量最多就 10^4 个了(规定只能是数字)，而如果整个 path 的长度再有限制(比如说 20)，那么自然嵌套的层级也有限制了(这里是 5 层)。

所以说这些都是取决于是如何设计的。

Nested Sets(嵌套集合)

先上一张图来理解这个模型：

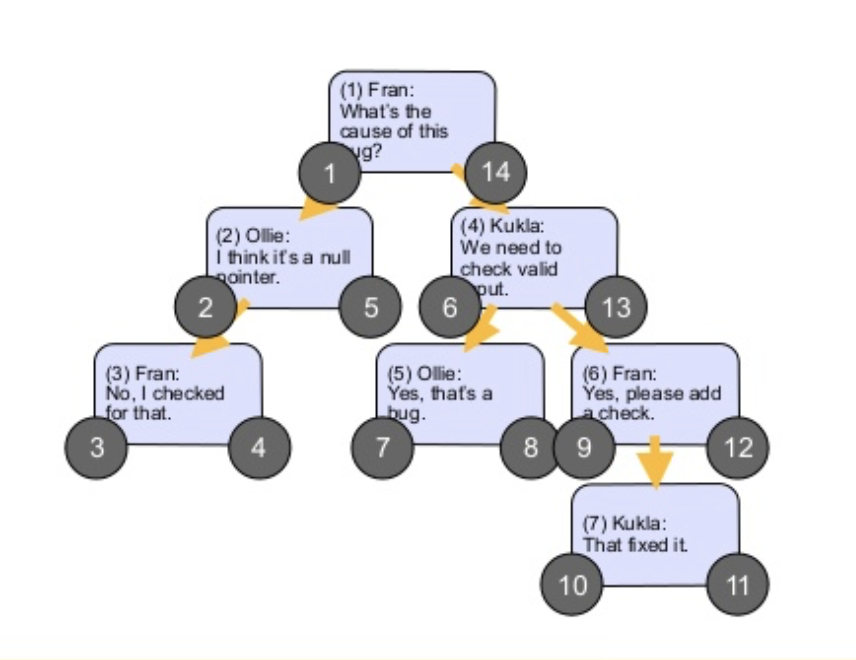
Nested Sets

可以看到每个节点都有一个 left 和一个 right，这是代表这个节点所能容纳的范围的，一个节点的 left 比它所有后代的 left 要小，一个节点的 right 比它所有后代的 right 要大。

添加/修改

添加和修改是十分复杂的，都需要重新计算节点的 left 与 right。

拿添加来说，比如给上图中第 5 个节点(它的left为left-5，right为right-5)添加子节点，那么需要做的就是把 right 大或等于 right-5 的节点都取出来，如果 left 大于或等于 right-5 那么就加 2，否则不变；right 全部都加 2；然后把新的节点 left 设为 right-5，right 设为 right-5 + 1，如下图：

Nested Sets add new node

删除

同样的删除也是非常复杂的，这也需要重新计算 left 和 right。

查询

查询一颗子树是非常方便的，只需要找出所有的 left 比该节点大，right 比该节点小的所有节点就可以了。

1
2
3

select *
from comments
where left > 1 and right < 14

元素数量和嵌套的层级

和邻接链表一样的。

总结

模型	查询子节点	查询子树	删除节点	插入节点	移动子树
Adjacency List	易	难(递归还好，相对耗时)	易	易	易
Materialized Path	难	易	易	易	易(但耗时)
Nested Sets	难	易	难	难	难

邻接链表是较为简单的一种实现，但是想要查询一颗树的时候会有很多阻力，如 Mysql 8.0 以下原生是不支持递归查询的(可以自定义函数来完成这个递归操作，详情看这里)，但是 Oracle、PostgreSQL、SQL Server 是支持的，除此之外，查询子树时存在查询效率问题(因为需要递归)。所以当你使用的场景插入或更新或删除较多的话是最好选择邻接链表模型的。如果查询树特别多，则可以使用嵌套集合模型或者物化路径模型(物化路径模型当层次较深的时候额外存储空间较大需谨慎)较为合适，当然如果使用的数据库原生支持递归语法，那么使用邻接链表模型也未尝不可，只是性能上会差一点。

总之还是根据具体情况具体分析，选择合适的才是最好的。